Programming Languages
静态程序分析是编程语言中应用层面下的一个细分领域,它是一个非常重要的核心内容。
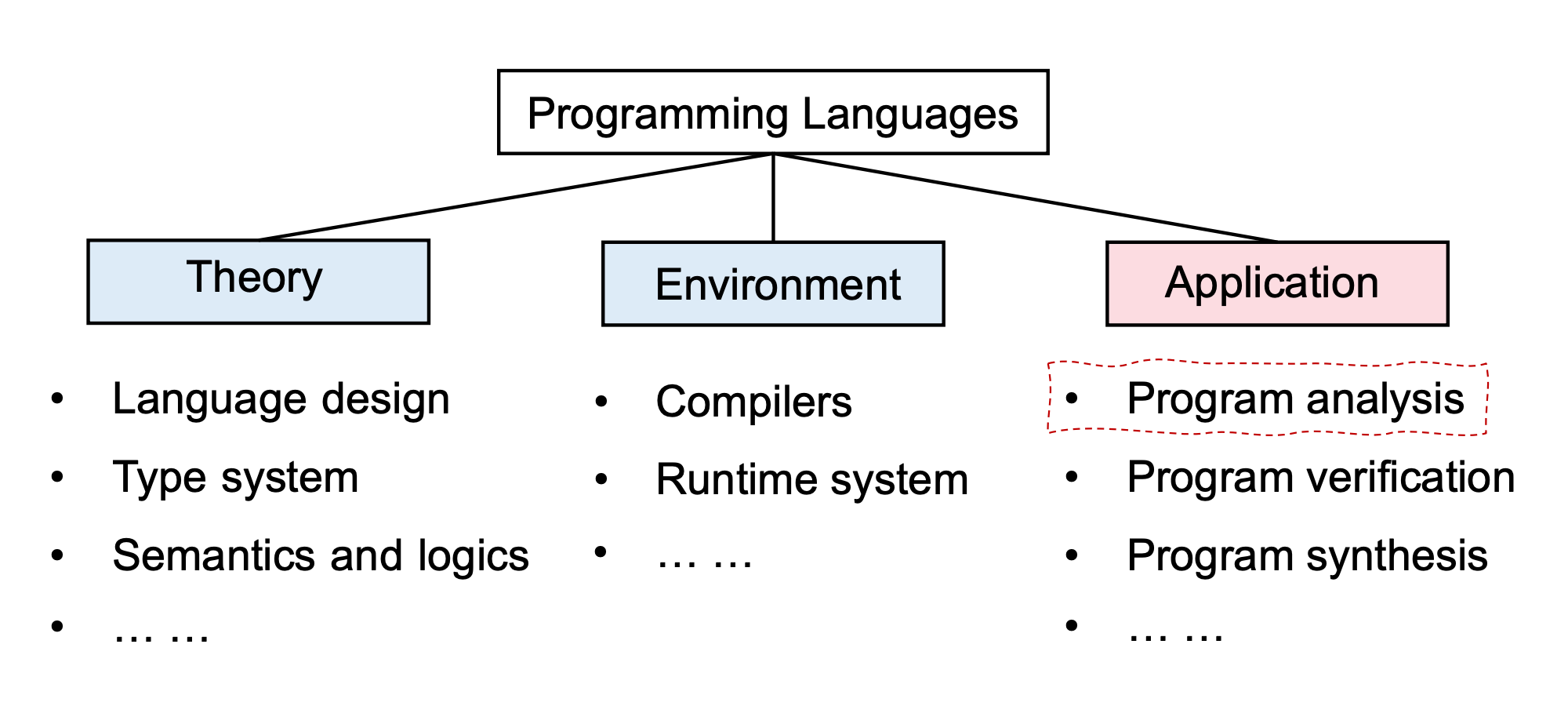
Programming Languages可以大致分为三个部分:
- 在理论部分,考虑的是如何设计一个语言的语法和语义,如何设计语言的类型系统等等问题。
- 在环境部分,由于已经有了语言的语法、语义和类型系统,需要支撑语言的运行,因此需要考虑如何为运行中的程序提供运行时环境,即如何设计编译器,在运行时需要怎样的支持(如内存的分配管理)等等。
- 在应用部分,则需要关注如何保证语言所写出程序的效率、安全性和可靠性,主要考虑如何对程序进行分析,验证和合成(如何自动合成一个程序)。
Background & Challenge
Background: In the last decade, the language cores had few changes, but the programs became significantly larger and more complicated.
Challenge: How to ensure the reliability, security and other promises of large-scale and complex programs?
Necessity
- 提高程序可靠性:空指针引用,内存泄漏等。
- 提高程序安全性:隐私信息泄露、注入攻击等。
- 编译优化:消除程序死代码(不会对程序执行结果产生影响的代码)、代码移动(通过重新排列指令来提高程序的性能,通常发生在编译器的中间代码生成或优化阶段)等。
- 提高程序可读性:集成开发环境(IDE)、代码调用层级(Call Hierarchy)、类型指示(Type Indication)等。
Static Program Analysis
简单来说,静态分析就是通过分析程序来推断其行为,并在运行程序之前确定该程序是否满足某些属性。(Static analysis analyzes a program P to reason about its behaviors and determines whether it satisfies some properties before running P)例如:
- 程序是否包含任何隐私信息泄露?
- 程序是否引用任何空指针?
- 程序中的所有强制转换操作是否安全?
- 程序中的指针1和指针2可以指向相同的内存位置吗?
- 程序中的某些断言语句会失败吗?
- 程序中的这段代码是死的吗(这样它就可以被消除)?
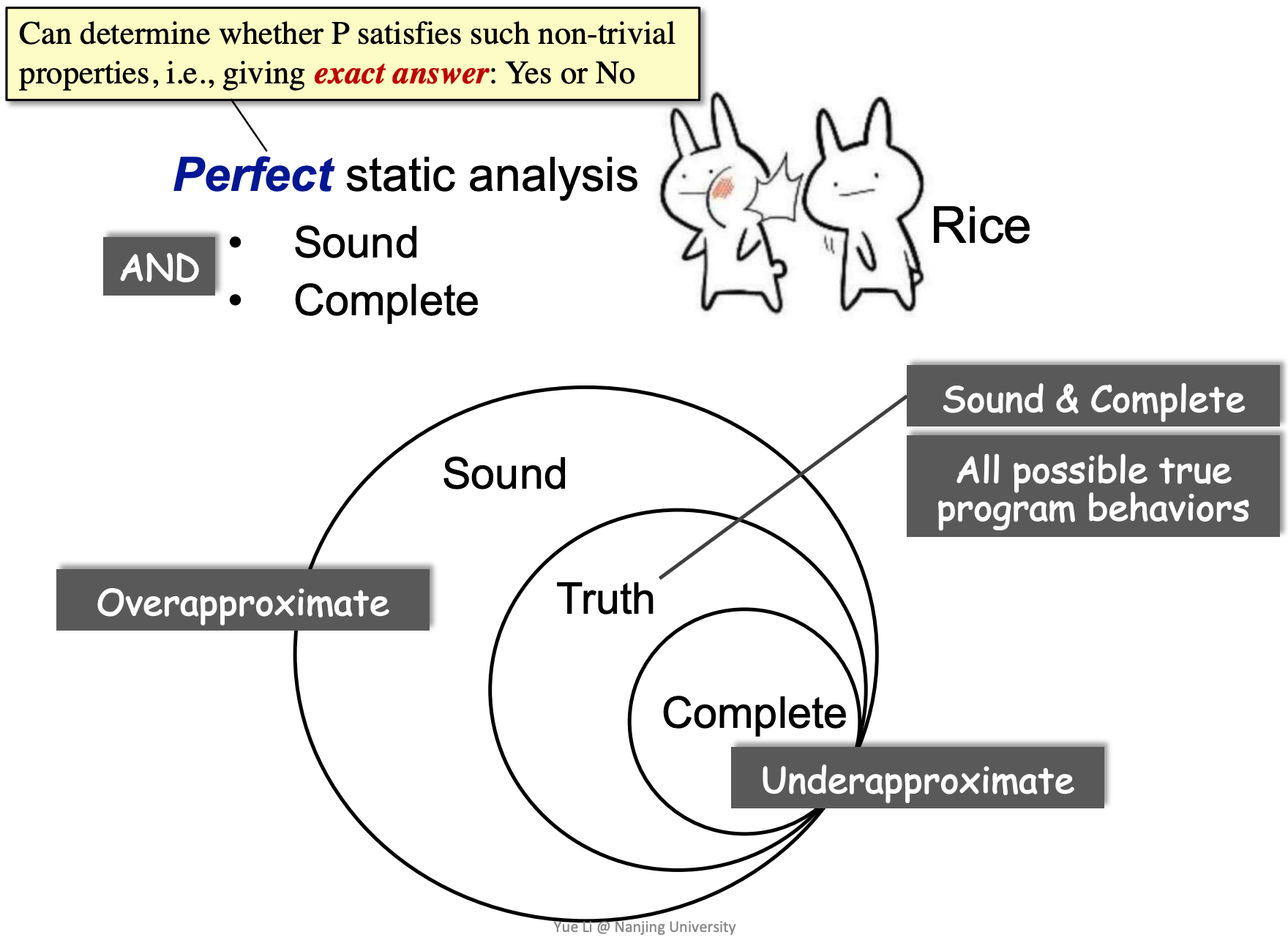
Rice’s Theorem: Any non-trivial property of the behavior of programs in a r.e. language is undecidable.
Rice’s Theorem(莱斯定理)证明,对于任何非平凡的部分函数属性,不存在一种通用且有效的方法来决定一个算法是否计算具有该属性的部分函数。换句话说,没有有效的方法仅通过查看程序代码即可确定函数的非平凡属性(即上述示例中提到的空指针引用、隐私信息泄露等)。

进一步理解,在下图中,莱斯定理指出不存在一个Perfect Static Analysis(例如空指针问题中,Perfect Static Analysis指的就是能够准确地给出是否存在空指针漏洞,存在几个空指针漏洞等)。
一个Perfect Static Analysis必须满足Sound又Complete。具体地说, Truth可以理解为程序中有N个空指针漏洞;Sound表示报告包含了所有的真实错误,但可能包含了误报的错误;Complete表示报告包含的错误都是真实的错误,但可能并未包含全部的错误。那么Sound、Truth和Complete之间的关系为Complete ⊆ Truth ⊆ Sound,Sound称之为over-approximate,Complete称之为under-approximate。
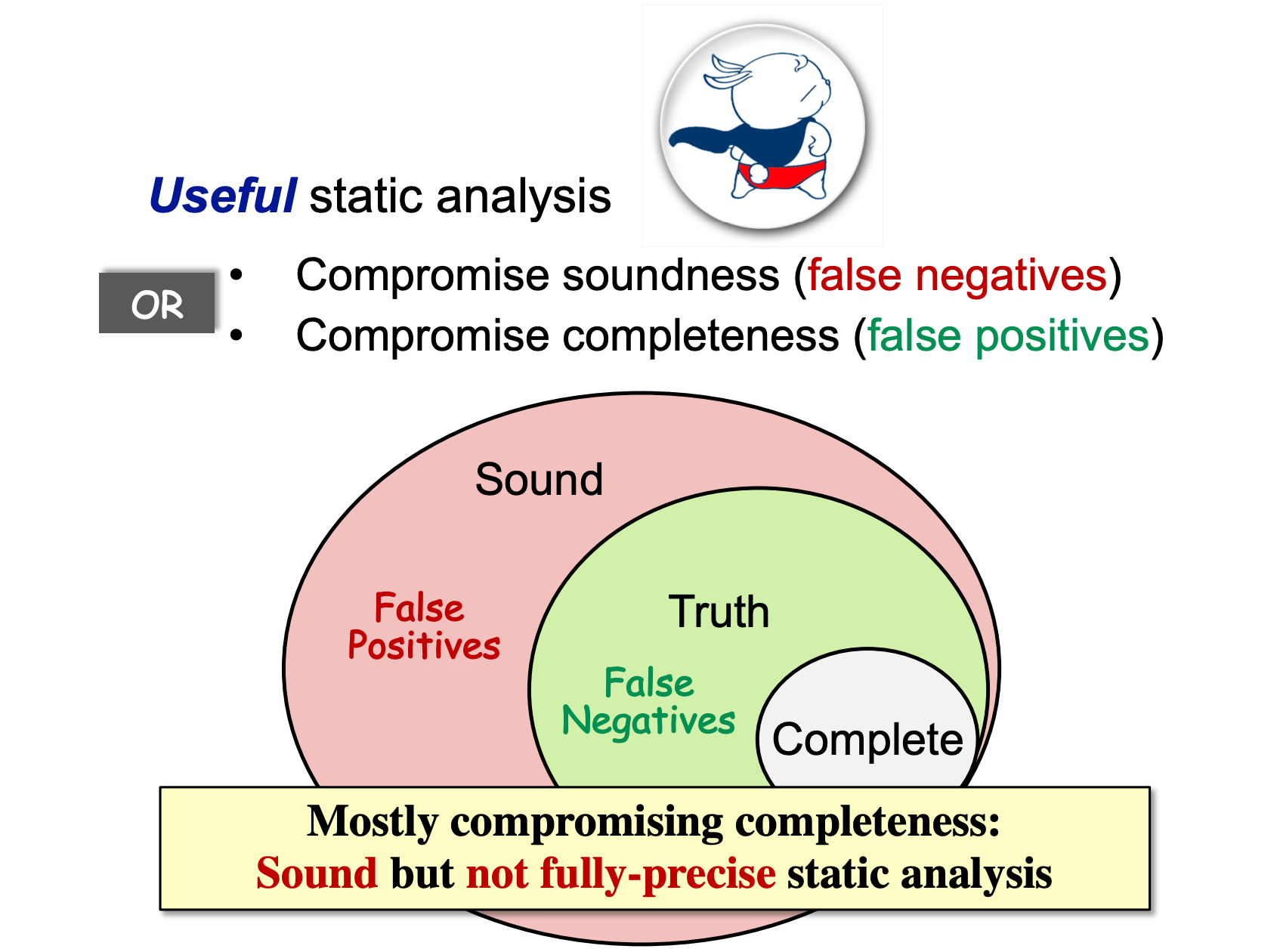
既然不存在Perfect Static Analysis,即无法同时满足Sound和Complete,那么可以妥协其中一方,在某种程度上牺牲Sound或Complete中的一个,即Useful Static Analysis。

在Useful Static Analysis中,妥协soundness,会造成false negatives(漏报);妥协completeness,会造成false positives(误报)。
通常情况下,静态分析时总是选择牺牲completeness,保全soundness。即,宁可有误报,也不漏掉一个正确结果。
那么为什么总选择保全Soundness呢?
- Soundness is critical to a collection of important (static-analysis) applications, such as compiler optimization and program verification.
- Soundness is also preferable to other (static-analysis) applications for which soundness is not demanded, e.g., bug detection, as better soundness implies more bugs could be found.
Example
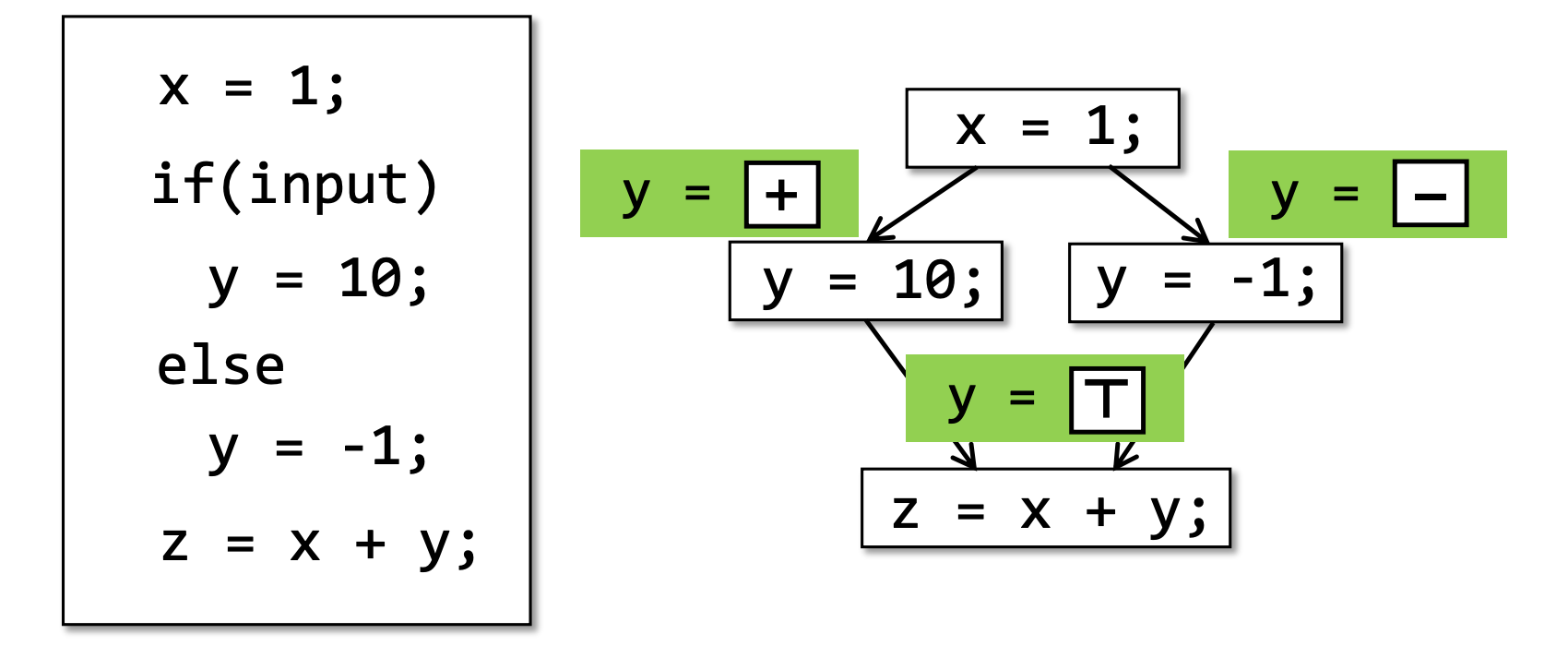
在下图示例代码中,存在两种不同表述的分析结果:
- 当input为true时,x等于1;当input为false时,x等于0。
- x等于1或0。
但是这两个分析都是sound的,区别在于,前者结果更精确,但是耗时长;后者结果不精确,但是速度快。因此,静态分析时通常需要尽力确保soundness,并在precision和speed之间做取舍。

Abstraction & Over-approximation
大多数静态分析都可以用abstraction和over-approximation两个词概括,而后者又包含transfer functions和control flows。

Abstraction是指将变量从concrete domain映射到abstract domain(符合集合),方便后续处理。由于在程序中,变量很可能是不确定的(unknown)或非法、未定义(undefined)的。因此,abstract domain包含五类符号+−O⊤⊥,其中⊤表示unknown,⊥表示undefined。
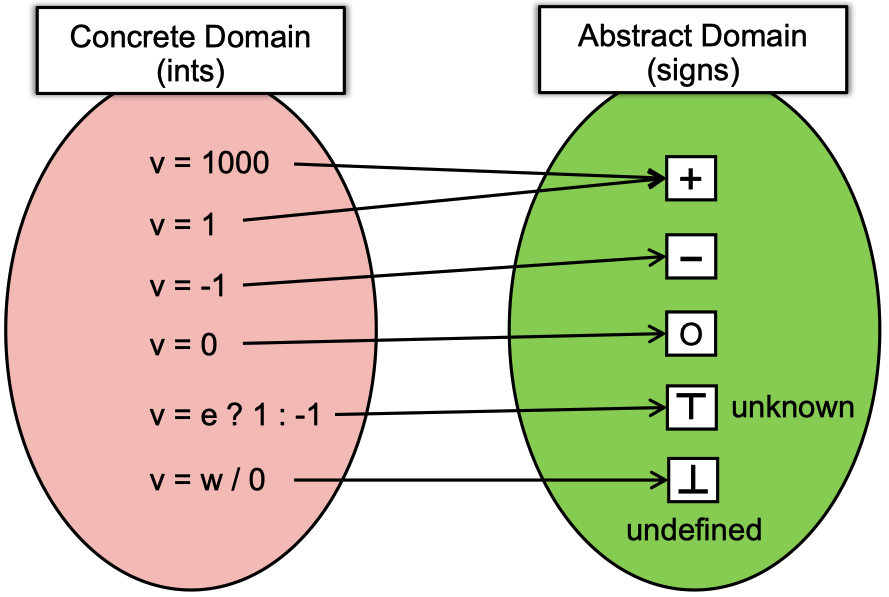
Over-approximation中的transfer functions定义了怎样在abstract values上对程序语句求值。transfer functions通常根据要分析的问题和程序语句相关的语义确定。对于算数运算,相关的transfer functions可以由算术运算规则和特性生成。
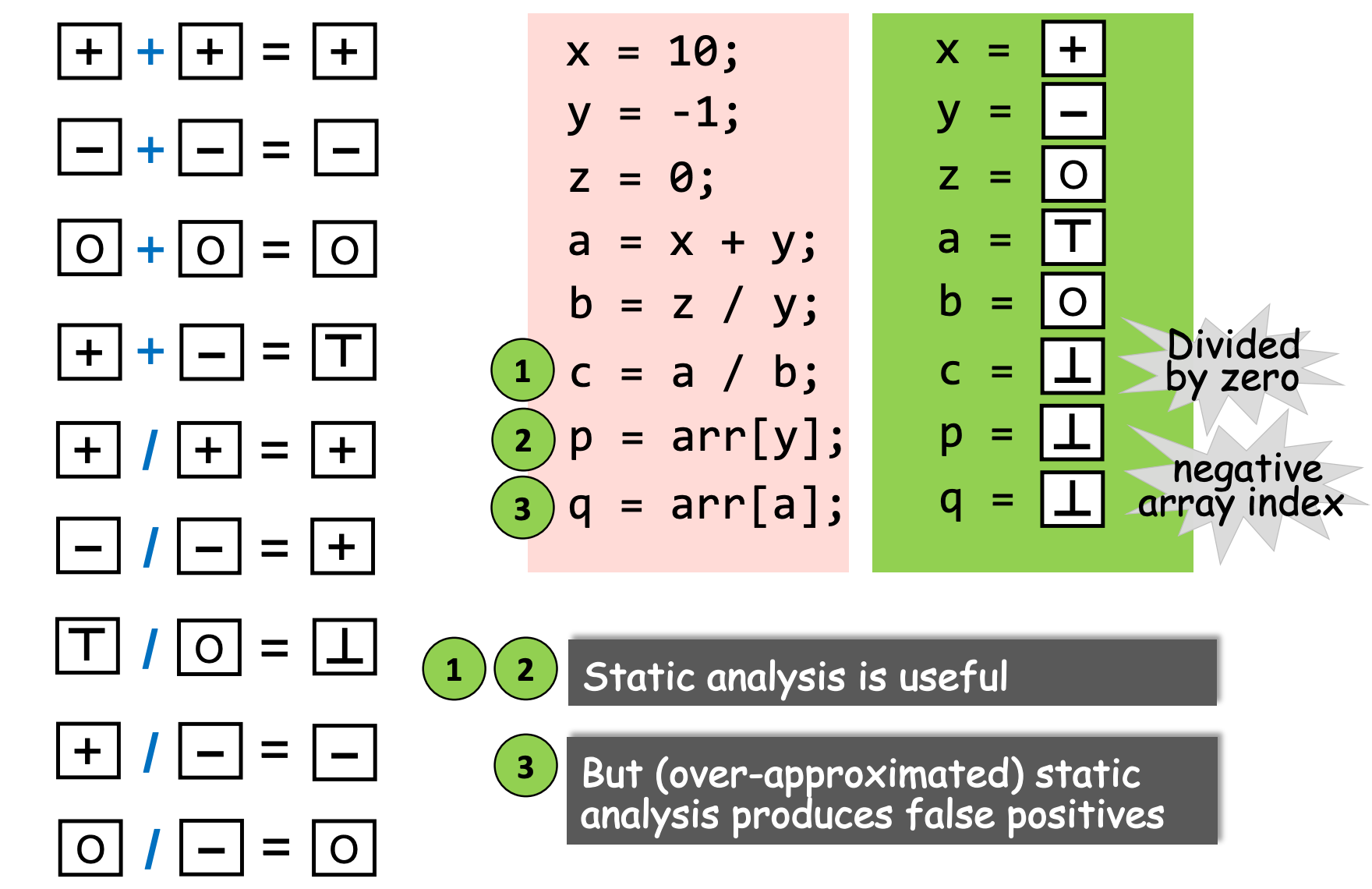
Over-approximation中的control flows指的是,在实际场景中进行控制流相关的静态分析时,由于无法枚举所有路径,我们通常采用flow merging(一种over-approximation的方式)来处理。